|
|

|
|
Nu när vi kan uppskatta klubbans fart vid bollträffen är det dags att se vad som händer vid själva kollisionen. Vilken typ av stöt har vi att göra med? Är den elastisk eller oelastisk? Detta är inte helt lätt att studera. Vid själva stöten händer nämligen en hel del, och detta på mindre än en tusendels sekund. Att klubban inte rör sig mer än en ett par cm under detta tidsintervall gör inte saken lättare. Till att börja med saktas klubbhuvudet ner, och bollen skickas iväg med mycket hög utgångshastighet med en vinkel i förhållande till horisontalplanet, och detta med riklig spinn. Man har visat att medelkraften mellan bollen och klubbhuvudet vid kollisionen är större än 13 350 N. Höghastighetfotografering har dessutom avslöjat att bollen trycks ihop ordentligt. Detta ger oss att stöten är oelastisk. För att klarlägga begreppet elastisk stöt kanske vi skall ta ett exempel. Tänk dig att ni släpper en boll från en viss höjd. Den studsar med största sannolikhet inte tillbaka ända upp till utgångsläget. Detta beror på att en studsboll är mjuk, och plattas ihop vid kollisionen med golvet. För att platta till bollen krävs energi, vilken då måste tas från rörelseenergin. För att bevara energimängden återvänder därför bollen med mindre rörelseenergi, alltså inte lika högt. Detta är en typisk oelastisk stöt. Om bollen däremot studsat till samma höjd betyder det att rörelseenergin behölls genom kollisionen, ingen energi behövde omvandlas till någon annan form, vilket skulle känneteckna en perfekt elastisk stöt. En sådan existerar emellertid inte i praktiken. Att stöten är oelastisk gör det hela mycket svårare att räkna på. Att det dessutom är friktion mellan bollen och träffytan hjälper oss inte heller. Denna friktion är emellertid "självförvållad". Har du någon gång sett träffytan på en golfklubba vet du att den är är räfflad. Dessa räfflor kallas "Grooves", och är till för att skapa just friktion, men bara i horisontalled. På golfbanan vill vi ju ha en viss spinn på bollen. Varför kommer att behandlas i nästa kapitel, men jag kan skvallra lite genom att säga att det har med lyftkraft att göra, och även lite med "back-spinn". Nu har vi helt klart ett inressant utgångsläge för att studera bollträffen djupare.
Rörelsemänden är konserveradVi börjar, som alltid då det gäller fysikaliska analyser, med att förenkla situationen något, d.v.s. med att bortse från vissa faktorers inverkan. Vad man däremot inte får glömma är att vara väl medveten om att resultatet inte stämmer helt med verkligheten. I avsnittet om svingen betraktade vi skaftet som "styvt". Detta var för att förenkla själva svingsituationen. När vi nu kommer till kollisionen, där nästan 13 350 N verkar mellan kropparna kan vi emellertid se skaftet som förhållandevis "mjukt". Detta medför att vi kan jämföra klubbhuvudets horisontella rörelse i den nedre delen av svingen med en fri kropps rörelse. Detta ger oss att klubbhuvudet och bollen efter stöten tillsammans har samma horisontella rörelsemängd som klubbhuvudet ensamt hade innan. Detta helt enligt lagen om rörelsemängdens bevarande. Den vertikala rörelsemängden kan vi emellertid inte betrakta enbart hos klubban och bollen. Den går nämligen delvis åt längs skaftet, då golfspelaren "drar" i klubban. För att uppskatta kraften i stöten kommer vi alltså att begränsa oss till den horisontella rörelsemängden då vi räknar på det. Att vi förenklar situationen kan verka lite "fegt", men om ni tänker efter så är det ingen dålig approximation, för hur stor inverkan har egentligen den vertikala rörelsemängden, jämfört med den horisontella? Ur följande ekvation kan vi ta fram bollens rörelsemängd efter bollträffen. Mv1 = Mv2 + mw cos a M representerar klubbhuvudets massa, medan m betecknar bollens massa. Hastigheterna v1 & v2hänvisar till klubbhuvudets hastighet före respektive efter bollträffen, och w till bollens hastighet. Beteckningarna återfinns även i bilden nedan.
Kollisionen är oelastiskNu när vi har en hygglig uppfattning om bollens rörlesemängd kommer vi till nästa problem, den oelastiska stöten. Som vi nämnde tidigare är det inte lätt att räkna på oelastiska stötar. Det hindrade emellertid inte Newton att redan under slutet av 1600-talet formulera en approximativ lag för den här typen av stötar. Experimenten gick till som i exemplet med bollen tidigare. Man undersökte alltså stöten då man studsade en boll mot golvet. Ur detta fann Newton att förhållandet mellan den hastighet bollen lämnar golvet med och bollens fallhastighet mot golvet är nästan konstant. Denna konstant kallas på engelska coefficient of restitution, vilket skulle kunna översättas till övergångskoefficient, och betecknas med e. För perfekt elastiska stötar är konstanten 1, medan den för en boll som inte studsar alls är 0. Så här kan man ställa upp Newtons ekvation för konstanten e.
Genom åren har det sedan visat sig att denna regel kan tillämpas även vid kollisioner där bollen lämnar ett slätt golv med en vinkel. Detta betyder att vi skulle kunna använda samma regel då vi analyserar kollisionen mellan bollen och klubbhuvudet, om träffytan vore slät vill säga. Som vi nämnde innan har vi emellertid "grooves" på träffytan, vilket ställer till det lite grann. Detta är vårt tredje problem, friktionen vid bollträffen. Innan vi tar tag i det kan vi göra en approxiamtion för bollens elastiska egenskaper, där vi approximerar bort denna friktion. Detta får vi dock se som en grov approximation, men det ger oss ändå en bra bild av händelseförloppet. För att tillämpa Newtons lag på en situation med infallsvinkel "avbildar" man de båda hastigheterna på Normalen till "golvet", i vårt fall klubbhuvudet. Enkel trigonometri ger oss då en formel enligt följande:
Vi använder samma skiss som då vi tittade på rörelsemängden i systemet, med skillnaden att vi betraktar klubban som stilla, och bollen som rörlig. Vi byter alltså inertialsystem. Det kan då vara på sin plats att förklara begreppet inertialsystem. Vi tar Knatte, Fnatte & Tjatte till hjälp. Knatte släpper en boll från axelhöjd, vilken studsar på golvet. Fnatte står bredvid och ser det hela som att bollen krockar med jorden, som för honom står stilla. Tjatte däremot betraktar händelseförloppet från rymden. Han ser det hela som att jorden krockar med bollen, som står stilla. Detta på grund av att han befinner sig i ett annat inertialsystem. 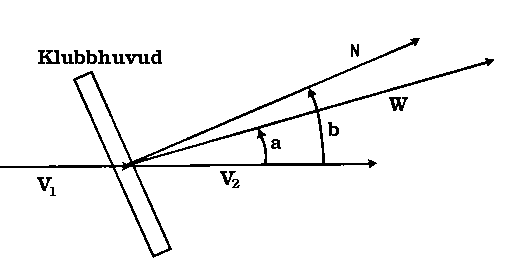
Jämför nu bollens rörelse från höger mot klubban, med en boll som vi "släpper" med en viss vinkel mot ett slätt golv. Infallshastigheten motsvarar då klubbans hastighet v1, fast med vinkeln b, alltså blir nämnaren, u1, i Newton ekvation v1 cos b. Täljaren u2 tar på samma sätt formen w cos(b-a) - v2 cos b då vi har en given utgångsvinkel. Vän av ordning kan nu ställa sig frågan, varför bollen inte studsar ut med samma vinkel mot normalen, precis som en ljusstråle gör mot en spegel. Då man använder formeln vill man ju ha vinklar som ingångsvärden, annars är de ju ointressanta. Dessa vinklar, då det gäller bollträffen, är inte helt lätta att mäta fram. Vid fotografering av bollträffen har man dock funnit att utgångsvinkeln är något "lägre" än träffytans normal. Förklaringen till detta ligger med största sannolikhet i vårt tredje problem, friktionen. Newtons formel fungerade ju inte riktigt då "golvet" inte var slätt, men vi får i alla fall en hygglig bild av bollens elastiska egenskaper.
FriktionFriktionen är som vi tidigare nämnde nödvändig då vi utövar den ädla sporten, men en riktig pina då vi analyserar händelseförloppet fysikaliskt. Då klubbhuvudet träffar bollen börjar bollen glida uppför träffytan, med en gradvis ökande friktionskraft. Denna friktionskraft resulterar i att bollen gradvis slutar glida och istället börjar "rulla". När den sedan lämnar klubbhuvudet kommer den ha slutat glida helt, och rullar (spinner) enbart. Detta förutsatt att friktionen var tillräcklig. Allt detta sker ju som sagt på mindre än en 1000-dels sekund, men händelseförloppet är jämförbart med ett bowlingklot på en bowlingbana. Till en början glider klotet på banan. Friktionskraften mellan banan och klotet saktar ned klotets rörelse. I samma takt börjar klotet rulla istället, och efter ett tag rullar det utan att glida. Den väsentliga skillanden mellan bowlingklotet och golfbollen är emellertid att klotet inte plattas ned märkbart mot banan, medan golfbollen plattas ihop till närmare halva diametern. Hur mycket den plattas till kan vi dock inte bestämma mer nogrannt än så. Detta ger oss problem då vi nu vill beräkna den spinn bollen har kring en horisontell axel vinkelrät mot träffytan. Angriper man det hela teoretiskt och försöker beräkna det med kända fysikaliska lagar tvingas man approximera ganska grovt. En lite mer praktisk angreppsvinkel kan ge ett bättre resultat. Om vi istället fotograferar händelseförloppet med en höghastighetskamera, där vi känner kamerahastigheten, och tydligt kan se hur bollen roterar, blir matematiken genast enklare. På följande bild har vi uppfyllt dessa kriterier, texten på bollen visar tydligt hur den roterar, och kamerans kapacitet är känd.
Då så, nu vet vi ungefär vad som händer under den tusendels sekund som kollisionen äger rum. Då är det dags att se hur denna enorma spinn påverkar bollens flykt från klubbhuvudet. |
|
|
|